Все формулы для радиуса описанной окружности
Найти радиус описанной окружности треугольника по сторонам
 ,
,  ,
,  - стороны треугольника
- стороны треугольника
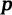 - полупериметр
- полупериметр
2.png)
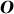 - центр окружности
- центр окружности
Формула радиуса описанной окружности треугольника ( R ) :
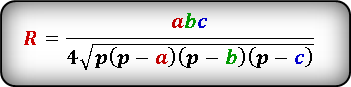
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
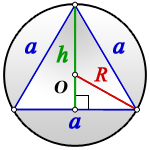
 - сторона треугольника
- сторона треугольника
 - высота
- высота
 - радиус описанной окружности
- радиус описанной окружности
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
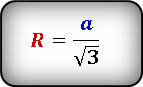
Формула радиуса описанной окружности равностороннего треугольника через высоту:
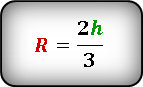
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
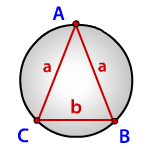
a, b - стороны треугольника
Формула радиуса описанной окружности равнобедренного треугольника(R):
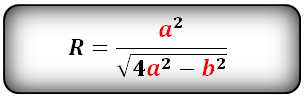
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
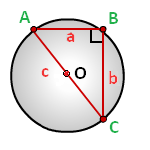
a, b - катеты прямоугольного треугольника
c - гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
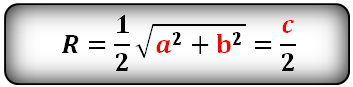
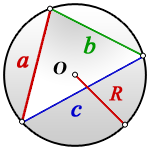
Радиус описанной окружности трапеции по сторонам и диагонали
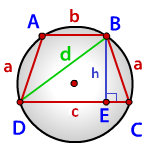
a - боковые стороны трапеции
c - нижнее основание
b - верхнее основание
d - диагональ
p - полупериметр треугольника DBC
p = (a+d+c)/2
Формула радиуса описанной окружности равнобокой трапеции, (R)

Найти радиус описанной окружности около квадрата
Радиус описанной окружности квадрата равен половине его диагонали
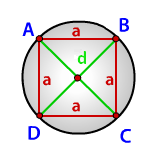
a - сторона квадрата
d - диагональ
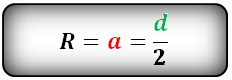
Формула радиуса описанной окружности квадрата (R):
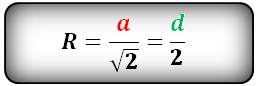
Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности прямоугольника равен половине его диагонали
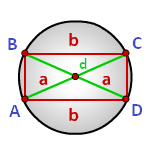
a, b - стороны прямоугольника
d - диагональ
Формула радиуса описанной окружности прямоугольника (R):
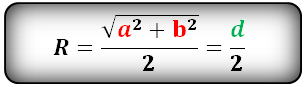
Радиус описанной окружности правильного многоугольника
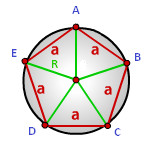
a - сторона многоугольника
N - количество сторон многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
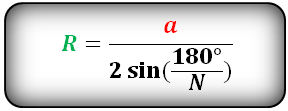
Радиус описанной окружности правильного шестиугольника
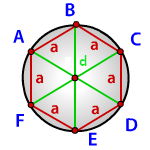
a - сторона шестиугольника
d - диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):