Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.

a, b - катеты
c - гипотенуза
α, β - острые углы
Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):


Формулы сторон по теореме Пифагора, (a,b):



Вычислить длину неизвестной стороны через любые стороны и углы

b - сторона (основание)
a - равные стороны
α - углы при основании
β - угол образованный равными сторонами
Формулы длины стороны (основания), (b):


Формулы длины равных сторон , (a):


Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a, b, c - стороны произвольного треугольника
α, β, γ - противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр - точка пересечения высот, совпадает с вершиной прямого угла.
 H - высота из прямого угла
H - высота из прямого угла
a, b - катеты
с - гипотенуза
c1 , c2 - отрезки полученные от деления гипотенузы, высотой
α, β - углы при гипотенузе
Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

Высота- перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется - ортоцентр.
 H - высота треугольника
H - высота треугольника
a - сторона, основание
b, c - стороны
β, γ - углы при основании
p - полупериметр, p=(a+b+c)/2
R - радиус описанной окружности
S - площадь треугольника
Формула длины высоты через стороны, (H):

Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через стороны и радиус, (H):

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M - медиана
R - радиус описанной окружности
O - центр описанной окружности
с - гипотенуза
a, b - катеты
α - острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):

Формула длины через катет и острый угол, (M):

Медиана - отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M - медиана, отрезок |AO|
c - сторона на которую ложится медиана
a, b - стороны треугольника
γ - угол CAB
Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L - высота=биссектриса=медиана
a - сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Калькулятор - вычислить, найти медиану, биссектрису, высоту
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.

L - высота = биссектриса = медиана
a - одинаковые стороны треугольника
b - основание
α - равные углы при основании
β - угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):



Формула высоты, биссектрисы и медианы, через стороны, (L):

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L - биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b - катеты прямоугольного треугольника
с - гипотенуза
α - угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через гипотенузу и угол, ( L):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L - биссектриса, отрезок ME , исходящий из острого угла
a, b - катеты прямоугольного треугольника
с - гипотенуза
α, β - углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):


Формула длины биссектрисы через катет и гипотенузу, (L):

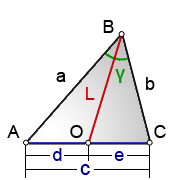
L- биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b - стороны треугольника
с - сторона на которую опущена биссектриса
d, e - отрезки полученные делением биссектрисы
γ - угол ABC , разделенный биссектрисой пополам
p - полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):

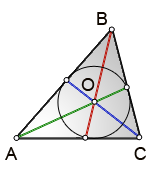
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

