Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
Высота - перпендикуляр исходящий из вершины угла на противоположенную сторону
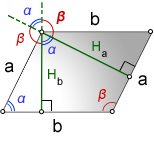a, b - стороны параллелограмма
Hb - высота на сторону b
Ha - высота на сторону a
α, β - углы параллелограмма
Формулы длины высоты параллелограмма, через сторону и угол, ( Hb, Ha):
Острый угол пересечения высот, равен острому углу параллелограмма.
Тупой угол пересечения высот, равен тупому углу параллелограмма.
Формулы площади параллелограмма
Формула периметра параллелограмма
Свойства биссектрисы параллелограмма
- Биссектриса по определению делит угол пополам
- Биссектриса отсекает равнобедренный треугольник (в данном случае треугольники ABF и DKC)
- Биссектрисы смежных углов, пересекаются под прямым углом (90°)
- Биссектрисы противоположных углов, равны и параллельны
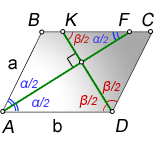AF - биссектриса из острого угла
DK - биссектриса из тупого угла
α - острый угол
β - тупой угол
a - меньшая сторона
b - большая сторона
Так как треугольники ABF и DKC, равнобедренные, следовательно справедливы тождества:
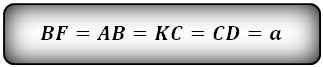
Длина биссектрисы параллелограмма
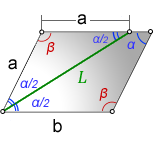
L - биссектриса параллелограмма
a, b - стороны
α, β - углы
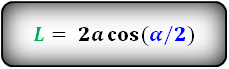
Формулы длины биссектрисы через сторону и углы, (L):
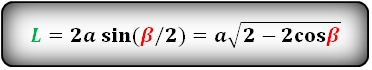
Формулы площади параллелограмма
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
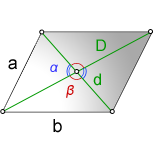
a, b - стороны параллелограмма
D - большая диагональ
d - меньшая диагональ
α - острый угол между диагоналями
β - тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
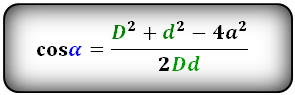
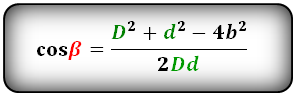
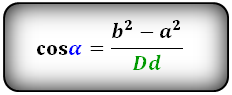
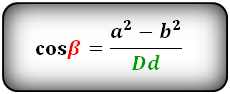
Формула синуса острого и тупого углов через площадь (S) и диагонали:
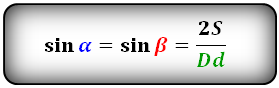
Формулы соотношения острого и тупого углов между диагоналями:
Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы площади параллелограмма
Свойства углов параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
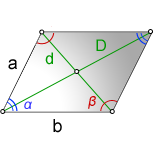
a, b - стороны параллелограмма
D - большая диагональ
d - меньшая диагональ
α - острый угол
β - тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):
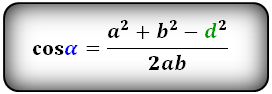
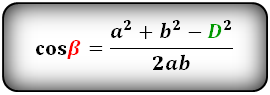
Формула синуса острого и тупого углов через площадь (S) и стороны:
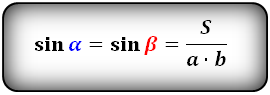
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b - стороны параллелограмма
D - большая диагональ
d - меньшая диагональ
α, β - углы параллелограмма
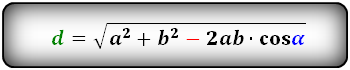
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
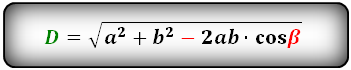
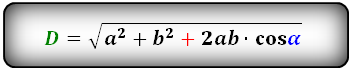
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
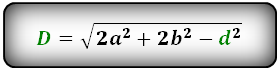
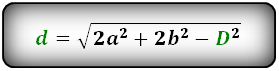
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D - большая диагональ
d - меньшая диагональ
α, β - углы между диагоналями
S - площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
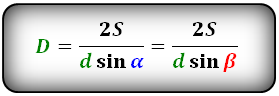
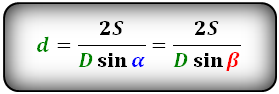
Формулы площади параллелограмма
Формулы суммы квадратов диагоналей и разности квадратов сторон параллелограмма:
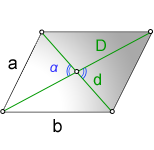
a, b - стороны параллелограмма
D - большая диагональ
d - меньшая диагональ
α - острый угол между диагоналями
Формула суммы квадратов диагоналей:
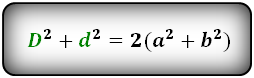
Формула разности квадратов сторон:
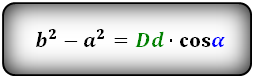
Формулы площади параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Формулы длины сторон через диагонали и угол между ними.
a, b - стороны параллелограмма
D - большая диагональ
d - меньшая диагональ
α, β - углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):
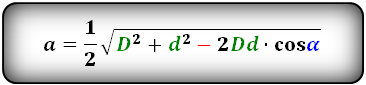
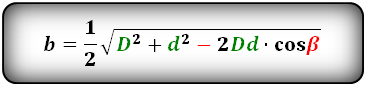
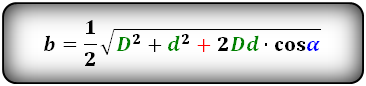
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
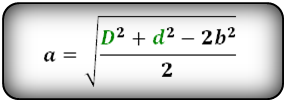
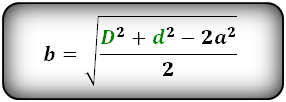
Формулы сторон параллелограмма , (a, b):
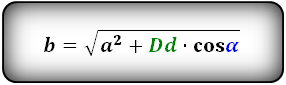
2. Формулы длины сторон параллелограмма через высоту.
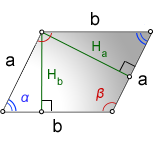
a, b - стороны параллелограмма
Hb - высота на сторону b
Ha - высота на сторону a
α, β - углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
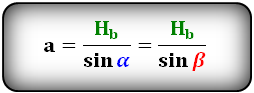
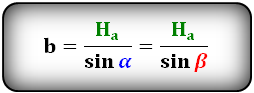
3. Дополнительные, интересные формулы параллелограмма:
a, b - стороны параллелограмма
D - большая диагональ
d - меньшая диагональ
α - острый угол между диагоналями
Формула суммы квадратов диагоналей:
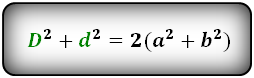
Формула разности квадратов сторон:
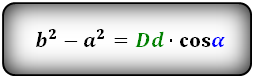
Формулы площади параллелограмма