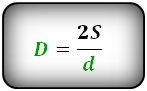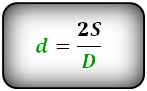Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
Свойства ромба:
1. Ромб - частный случай параллелограмма
2. Противоположные стороны - параллельны
3. Все четыре стороны - равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a - сторона ромба
D - большая диагональ
d - меньшая диагональ
α - острый угол
β - тупой угол
Формула стороны через диагонали, ( a ):
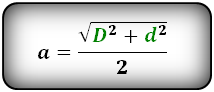
Формулы стороны через диагональ и угол, ( a ):
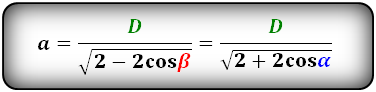
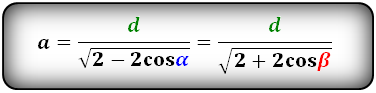
Формулы стороны через диагональ и половинный угол, ( a ):


Формулы стороны через диагонали и угол, ( a ):
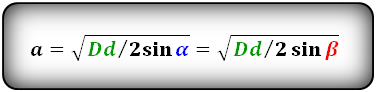
Формулы стороны через площадь ромба ( S ) и угол, ( a ):
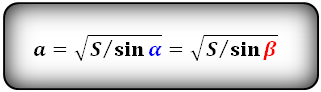
Формулы стороны через периметр ромба ( P ) и угол, ( a ):

Свойства ромба:
1. Ромб - частный случай параллелограмма
2. Противоположные стороны - параллельны
3. Все четыре стороны - равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a - сторона ромба
D - большая диагональ
d - меньшая диагональ
α - острый угол
β - тупой угол
Формулы косинуса углов через диагональ и сторону:
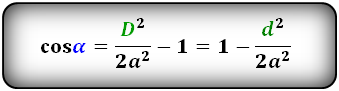
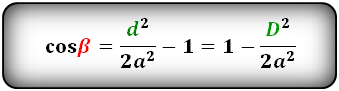
Формулы синуса углов через диагонали :
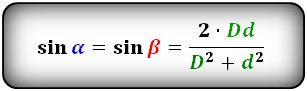
Формулы синуса углов через площадь S и сторону :
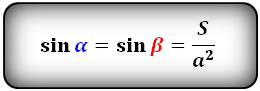
Формулы тангенса половинных углов через диагонали
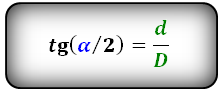
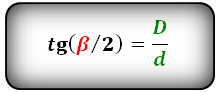
Формулы соотношения острого и тупого углов:

Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
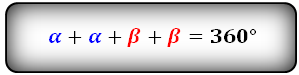
Свойства ромба:
1. Ромб - частный случай параллелограмма
2. Противоположные стороны - параллельны
3. Все четыре стороны - равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a - сторона ромба
D - большая диагональ
d - меньшая диагональ
α - острый угол
β - тупой угол
Формулы диагоналей через сторону и угол, ( D d):
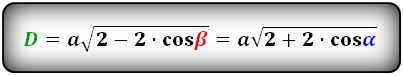
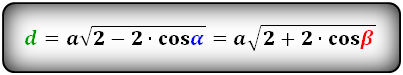
Формулы диагоналей через сторону и половинный угол, (D d):
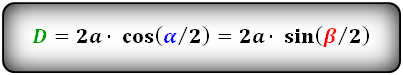
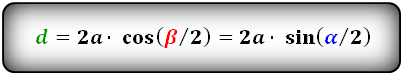
Формулы диагоналей через сторону и другую диагональ, (D d):


Формулы диагоналей через угол и другую диагональ, (D d):
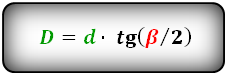
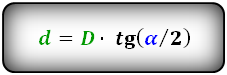
Формулы диагоналей через площадь (D d):