Все формулы объемов геометрических тел
1. Расчет объема куба

a - сторона куба
Формула объема куба, (V):

2. Найти по формуле, объем прямоугольного параллелепипеда

a, b, c - стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы

R - радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

4. Как вычислить объем цилиндра ?
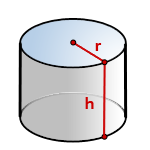
h - высота цилиндра
r - радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны - его радиус основания и высота, (V):

5. Как найти объем конуса ?
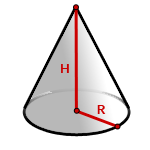
R - радиус основания
H - высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
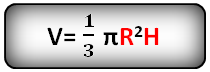
7. Формула объема усеченного конуса
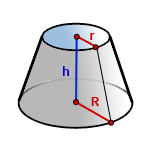
r - радиус верхнего основания
R - радиус нижнего основания
h - высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны - радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

8. Объем правильного тетраэдра
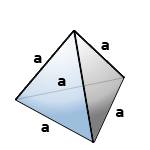
Правильный тетраэдр - пирамида у которой все грани, равносторонние треугольники.
а - ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
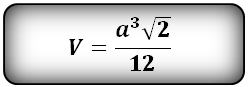
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
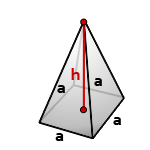
a - сторона основания
h - высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
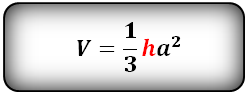
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
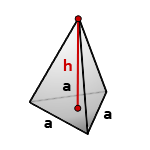
a - сторона основания
h - высота пирамиды
Формула объема правильной треугольной пирамиды, если даны - высота и сторона основания (V):

11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
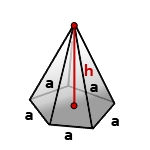
h - высота пирамиды
a - сторона основания пирамиды
n - количество сторон многоугольника в основании
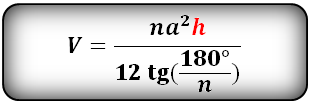
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
12. Расчет объема пирамиды
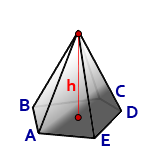
h - высота пирамиды
S - площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны - высота и площадь основания (V):
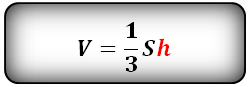
13. Расчёт объёма усечённой пирамиды
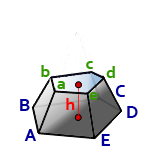
h - высота пирамиды
Sниж - площадь нижнего основания, ABCDE
Sверх - площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

14. Объем шарового сегмента, формула
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R - радиус шара
h - высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
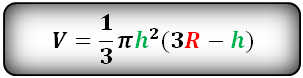
15. Объем шарового сектора
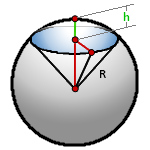
R - радиус шара
h - высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

16. Объем шарового слоя
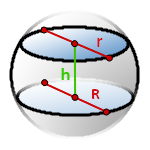
h - высота шарового слоя
R - радиус нижнего основания
r - радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):