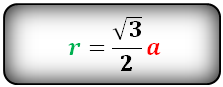Все формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
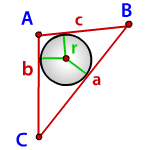
a, b, c - стороны треугольника
p - полупериметр, p=(a+b+c)/2
Формула радиуса вписанной окружности в треугольник (r):
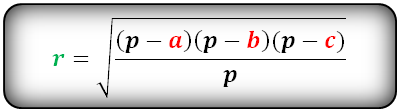
Радиус вписанной окружности в равносторонний треугольник
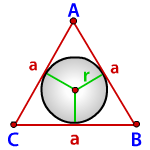
a - сторона треугольника
r - радиус вписанной окружности
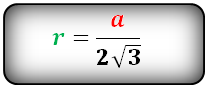
Формула для радиуса вписанной окружности в равносторонний треугольник (r):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
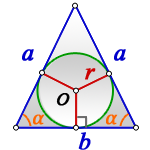
a - равные стороны равнобедренного треугольника
b - сторона ( основание)
α - угол при основании
О - центр вписанной окружности
r - радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
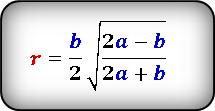
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
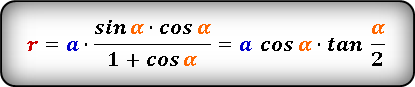
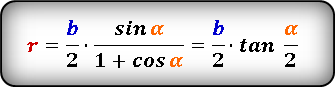
2. Формулы радиуса вписанной окружности если известны: сторона и высота
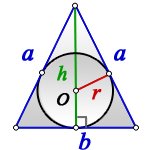
a - равные стороны равнобедренного треугольника
b - сторона ( основание)
h - высота
О - центр вписанной окружности
r - радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

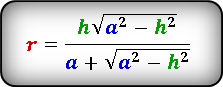
Радиус вписанной окружности в прямоугольный треугольник
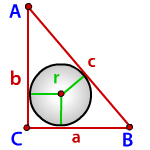
a, b - катеты треугольника
с - гипотенуза
Формула радиуса вписанной окружности в прямоугольный треугольник (r):
Радиус вписанной окружности в равнобочную трапецию
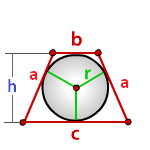
с - нижнее основание
b - верхнее основание
a - боковые стороны
h - высота
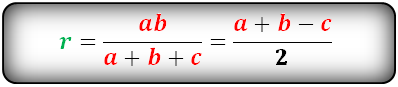
Формула радиуса вписанной окружности равнобочной трапеции (r):
Радиус вписанной окружности в квадрат
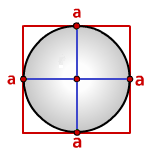
a - сторона квадрата
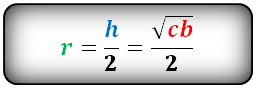
Формула радиуса вписанной окружности в квадрат (r):
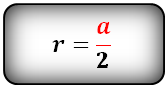
Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
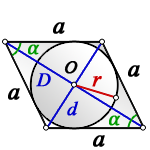
a - сторона ромба
D - большая диагональ
d - меньшая диагональ
α - острый угол
О - центр вписанной окружности
r - радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
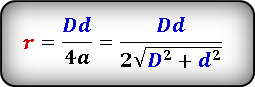
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
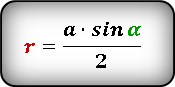
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
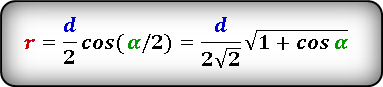
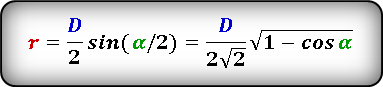
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
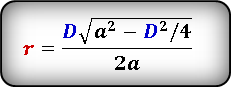
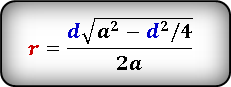
2. Радиус вписанной окружности ромба, равен половине его высоты
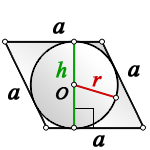
a - сторона ромба
h - высота
О - центр вписанной окружности
r - радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
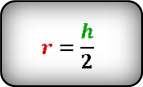
Радиус вписанной окружности в правильный многоугольник
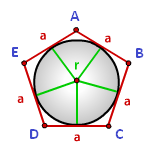
a - сторона многоугольника
N - количество сторон многоугольника
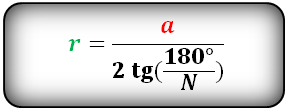
Формула радиуса вписанной окружности в правильный многоугольник, (r):
Радиус вписанной окружности в шестиугольник
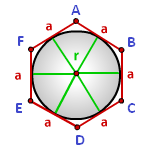
a - сторона шестиугольника
Формула радиуса вписанной окружности в шестиугольник, (r):