Условие задачи:
Прямоугольный треугольник вписан в окружность Найти площадь круга, ограниченного этой окружностью, если катет треугольника равен 2м, противоположный этому катету угол, составляет 30 градусов.
Дано:
Катет, a = 2 м
Противоположный угол, α = 30°
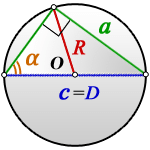
Пояснение к рисунку:
O - центр окружности
R - радиус описанной окружности
D - диаметр описанной окружности
c - гипотенуза треугольника
Найти площадь круга: S
Решение
Можно применить формулу площади круга через радиус или через диаметр. И мы воспользуемся формулой через диаметр, который пока мы не знаем.
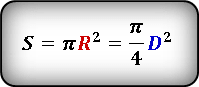
Но как известно, если прямоугольный треугольник вписан в окружность, то его гипотенуза равна диаметру окружности. Это так же видно и из рисунка. А зная катет и противоположный угол, мы можем найти гипотенузу треугольника, т. е. диаметр окружности. Далее, подставив значения, находим чему равен диаметр.
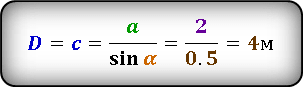
Теперь, зная диаметр, вычислим площадь круга.
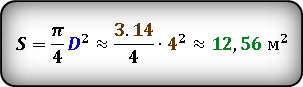
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Ответ:
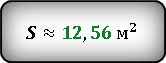
Калькулятор для расчета площади круга
