Условие задачи:
Равносторонний треугольник вписан в окружность. Найти площадь круга, ограниченного этой окружностью, если известно, что длина отрезка ОК равна 2 м.
Дано:
Отрезок, ОК = 2 м
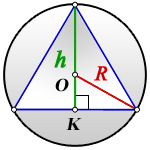
Пояснение к рисунку:
O - центр окружности
R - радиус описанной окружности
h - высота треугольника
Найти площадь круга: S
Решение
Используем формулу площади круга через радиус. Но пока он нам не известен, его надо найти.
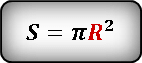
Определить радиус, нам поможет следующая формула. В ней он выражен через высоту вписанного треугольника, которую мы тоже пока не знаем.
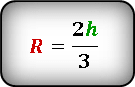
Но очевидно, что высота равна сумме радиуса и отрезка ОК.
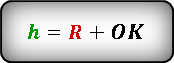
И уже на основании двух последних формул, подставим вместо высоты - сумму радиуса и отрезка ОК и преобразуем.
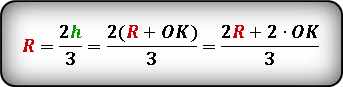
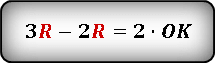
И на конец, получаем радиус окружности, выраженный через отрезок ОК.
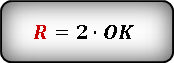
Теперь, вместо радиуса подставляем выражение которое мы вывели. В результате получаем формулу искомой площади круга через длину отрезка ОК.
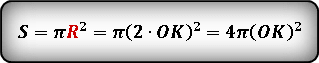
Вставляем значения.
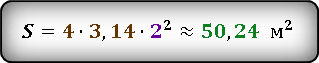
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Ответ:
Калькулятор для расчета площади круга
