Условие задачи:
В окружность вписан квадрат. Найти площадь закрашенной области, если радиус окружности равен 3 м.
Дано:
Радиус окружности, R = 3 м
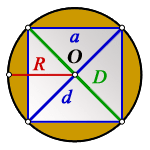
Пояснение к рисунку:
O - центр окружности
a - сторона квадрата
d - диагональ квадрата
D - диаметр окружности
Найти площадь закрашенной области: S
Решение
Площадь искомой области можно выразить как разницу между площадью круга и площадью квадрата
Площадь круга
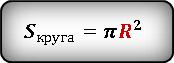
Площадь квадрата
Неизвестна сторона квадрата. Из рисунка видно, что диагональ квадрата равна диаметру окружности и соответственно удвоенному радиусу
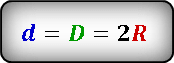
Сторону квадрата можно выразить через диагональ, используя следующую формулу. И вместо диагонали подставить радиус окружности.
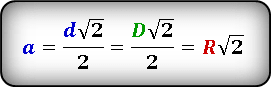
Теперь, формула площади квадрата через радиус окружности, будет выглядеть следующим образом.
Подставив уже известные формулы площади круга и квадрата выраженные через радиус, в самую первую формулу площади искомой области, получаем.
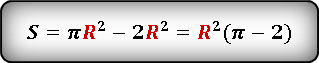
Вставляем значения.
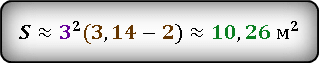
Ответ:
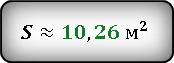
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Калькулятор для расчета закрашенной области
