Условие задачи:
Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.
Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см
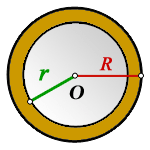
Пояснение к рисунку:
O - общий центр окружностей
Найти площадь кольца: S
Решение
Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.
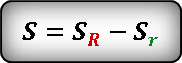
Формула площади внешнего круга.
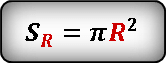
Формула площади внутреннего круга.
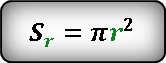
После подстановки и преобразования, получаем следующее выражение для площади кольца.
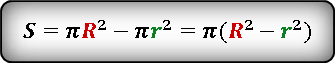
Вставляем значения.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Калькулятор для расчета площади кольца
